Merge sort
병합 정렬
Merge sort는 buble sort의 느린 속도를 해결하기 위해 만들어진 정렬 알고리즘
ex)
A: 2 5 7 10
B: 1 3 8 9
어떻게 A와 B를 합칠 수 있을까?
위 경우, 배열 A에는 [ 2 5 7 10]이 있고, 배열 B에는 [1 3 8 9]가 저장되어 있다.
(1) 만약, 이 배열이 각각 정렬되어 있다는 사실을 알고 있다면, A와 B를 합친 배열 [2 5 7 10 1 3 8 9]를 빠르게 정렬할 수 있게 된다. A 와 B 가 각각 정렬되어 있기 때문에, A + B 를 하였을 때의 최소 원소는 당연히 A 의 최소 원소거나, B 의 최소 원소가 될 것. 따라서, 단 한 번의 비교 만으로 A+ B 에 올 첫 번째 원소를 알아낼 수 있다.
(2) 만약, 정렬된 상태가 아니라면, A + B의 최소 원소를 알아내기 위해서 전체 배열을 순회해야한다. 즉, O(n)의 시간이 걸렸을 것이다. 하지만 A와 B가 정렬되어 있었기에 O(1)로 찾아낼 수 있다.
그렇다면 그 다음으로 작은 원소는 어떻게 찾을까. 방금 B의 원소 1을 A + B의 첫 번째 원소로 넣었으므로, 이제 B는 마치 [3 8 9]만 있다고 보면 된다. 따라서, 그 다음에 올 원소는 [2 5 7 10]과 [3 8 9]의 최소 원소 이므로 2가 오게 된다.
따라서 위의 방식대로 두 개의 정렬된 배열을 하나의 정렬된 배열로 합치는 작업은 각각의 원소당 O(1)로 할 수 있기에, 합친 배열의 원소의 개수가 n개라면 총O(n)의 시간 복잡도로 수정할 수 있다.
그렇다면 merge sort 함수를 이용해서 어떻게 전체 배열의 정렬을 수행할 수 있을까. 어찌되었든 병합을 하기 위해서는 정렬된 두 배열을 준비해야 되는데... 그러나 영원히 정렬을 못하는 것은 아니다. 왜냐하면 크기가 1인 배열은 이미 정렬된 상태로 간주할 수 있기 때문이다. 따라서 크기가 2인 배열을 정렬하기 위해서는 이를 반으로 나누어서 위의 merge함수를 호출하면 된다.
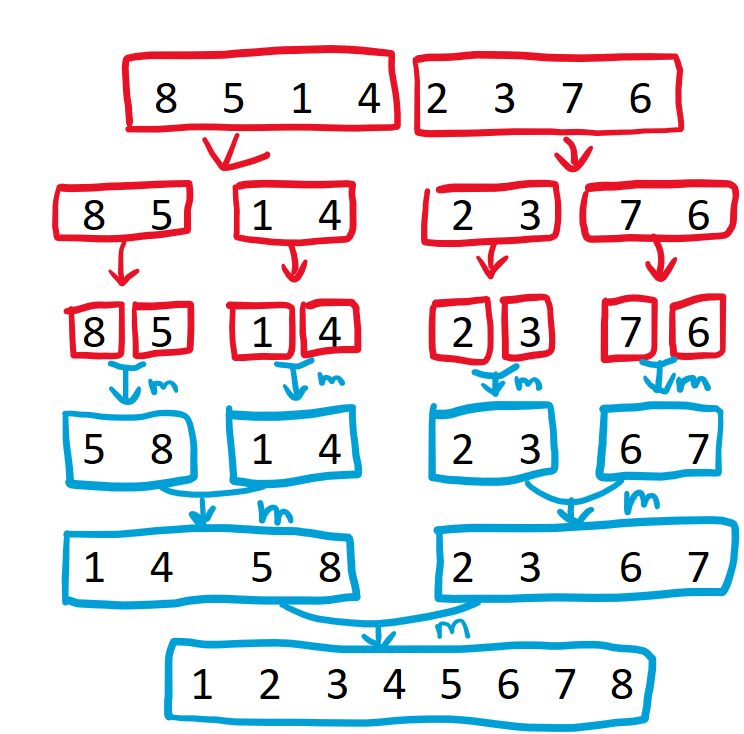
merge 함수를 호출하기 위해서는 이미 정렬된 두 배열을 준비해야 한다. 따라서, 위 경우 8, 5, 1, 4 와 2, 3, 7, 6 을 어떻게든 정렬을 해야지만 병합을 할 수 있게 된다.
마찬가지로 8, 5, 1, 4 를 정렬하기 위해서는 8, 5 와 1, 4 각각을 정렬을 해야지만 병합을 할 수 있게 된다.
마지막으로 8, 5 를 정렬하기 위해서는 8 과 5 각각을 정렬해야 하고, 1, 4 를 정렬하기 위해서는 1, 4 각각을 정렬해야 하는데, 원소 한 개 짜리 배열은 이미 정렬된 것으로 간주될 수 있으므로, 무사히 병합을 수행할 수 있게 된다.
이 부분이 위 그림에서 파란색으로 m 이라고 써있는 부분이다. 이제 5, 8 과 1, 4 로 각각 정렬되어 있으므로, 이를 다시 병합 하면 [8, 5, 1, 4] 의 정렬된 결과인 [1, 4, 5, 8] 을 얻을 수 있다. 마찬가지로 [2, 3, 7, 6] 부분 역시 정렬된 배열인 [2, 3, 6, 7] 을 얻을 수 있고, 마지막으로 다시 한 번 더 병합 한다면 [1, 2, 3, 4, 5, 6, 7, 8] 을 얻게 된다.

Merge sort A[1...n]
1. if n=1, done
2. Recursivery sort A[1...n/2)] and A[(n/2)+1...n]
3. "Merge" the 2 sorted lists.

이 알고리즘의 시간 복잡도는 어떻게 계산할까? 위 알고리즘에서 연산이 실행되는 부분은 앞서 그림에서 파란색으로 나타낸 merge 함수가 호출되는 부분이다.

merge 함수를 호출 하는 부분에서 실제 연산이 수행된다
그리고 앞서 merge 함수의 경우 합쳐진 배열의 크기가 n
n 이라면, merge 연산이 O(n)
O(n) 으로 수행된다는 사실을 알고 있다. 따라서, 위 정렬의 경우 각 단계에서 수행되는 연산의 회수는 다음과 같다.

각 단계에서 총 8 번의 연산을 수행한다
위 경우 첫 번째 단계에서 (1 개 짜리 배열 두 개를 2 개 짜리 배열로 합칠 때), 총 2×4=8 번의 연산을 수행. 그리고 두 번째 단계에서는 좀 더 큰 배열을 하나로 합치지만, merge 를 하는 횟수 자체는 절반으로 줄어들어서 총 4×2=8 번의 연산을 수행하고, 마지막 단계에서는 merge 한 번을 4 개 짜리 원소 배열 두 개를 합치는데 한 번 사용하기 때문에 8×1=8 번의 연산이 수행
따라서 총 24 번의 연산이 수행. 이를 일반화 시켜서 크기가 2n인 배열을 정렬할 경우 시간 복잡도가 어떻게 될지 생각해보자.
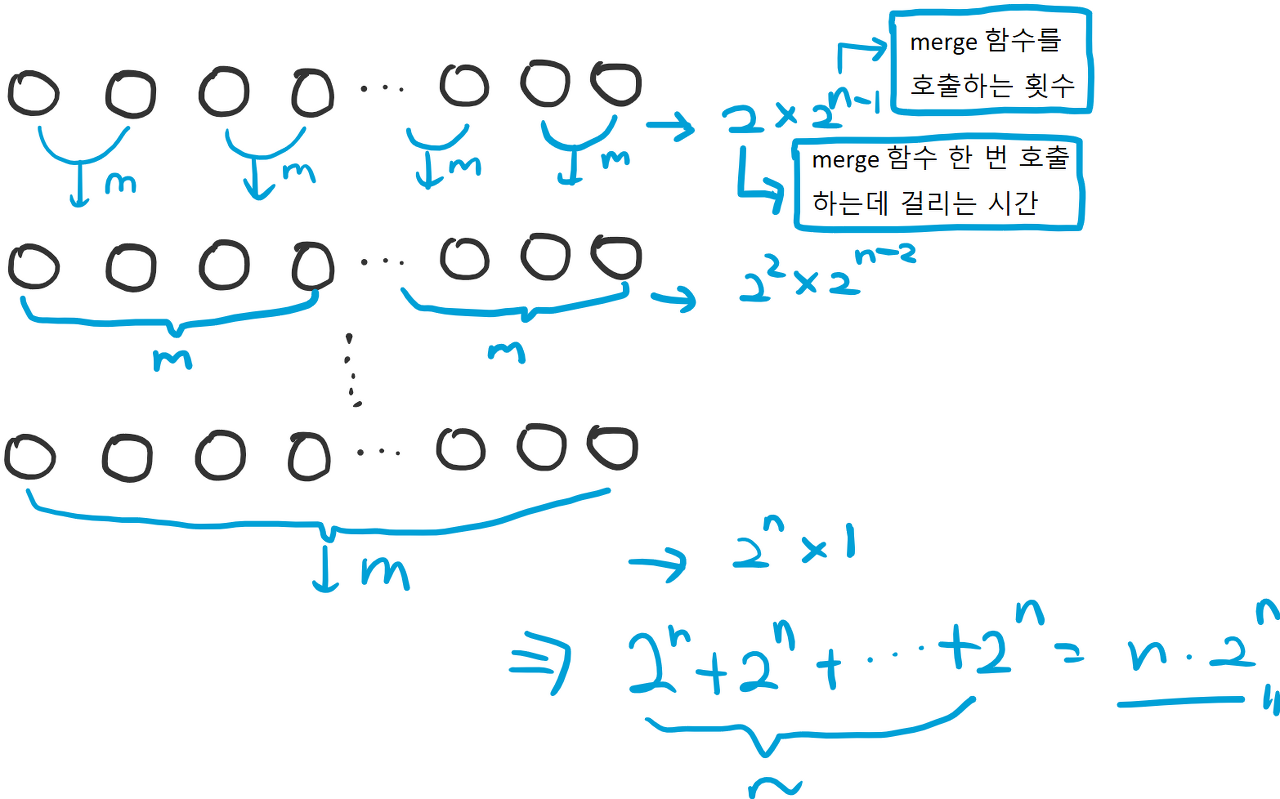
각 단계에서 총 8 번의 연산을 수행한다
첫 번째 단계에서는 크기가 2 인 배열로 merge 하는 작업을 총 2n−1 번 수행할 것. 그 다음 단계에서는 2 인 배열 두 개를 크기가 4=22 인 배열로 merge 하는 작업을 총 2n−2 번 함. 그 다음에는 크기가 23 인 배열로 merge 하는 작업을 2n−3 번 하고 맨 마지막에는 크기가 2n−1 인 정렬된 배열 두 개를 merge 하는 작업을 딱 한 번 할 것. 전체 시간 복잡도를 식으로 표현하자면 다음과 같음.
O(2)×2n−1+O(22)×2n−2+⋯+O(2n−1)×2+O(2n)×1=O(n⋅2n)
O(2)×2n−1+O(22)×2n−2+⋯+O(2n−1)×2+O(2n)×1=O(n⋅2n)
위는 배열 전체의 원소의 개수가 2n 개 였을 때의 시간 복잡도를 의미합니다. 따라서 만약에 원소의 개수가 n
n 개 였다면, O(nlogn) 번 걸렸을 것. (2n 이 n 에 대응되고, n 이 logn 에 대응됨)
따라서 이 병합 정렬의 전체 시간 복잡도는 O(nlogn) 이 된다. 이는 거품 정렬의 O(n2) 보다 훨씬 빠릅니다! 앞서 5천만명의 데이터를 정렬할 때, 병합 정렬을 사용하면 5×107×log(5×107)≈3.8×108 의 연산으로도 정렬할 수 있게 된다. 이는 대략 0.4 초 면 충분! 버블 소트의 경우 23 일 정도 걸렸음.
이것이 바로 좋은 알고리즘을 사용해야 하는 이유 입니다. 작업의 속도를 정말 믿을 수 없을 정도로 단축 시킬 수 있다.
'Study > C and AI' 카테고리의 다른 글
| tensorflow example 모듈 오류 (0) | 2021.05.21 |
|---|---|
| [OSS] 일단 CNN(Convolutional Neural Network)이 뭔데? (0) | 2021.05.21 |
| [Algorithms] 문자열 배열을 활용한 Palindrome (0) | 2021.05.21 |


댓글